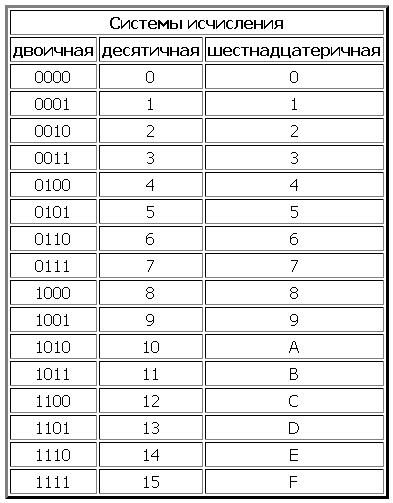
Системы исчисления: двоичная, восьмеричная, десятичная, шестнадцатеричная.

Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов (1 и 0). Компьютер может различить только нулевое и единичное состояние бита, и работает компьютер в системе исчисления с основанием 2 или в двоичной системе.

Сочетанием двоичных цифр (битов) можно представить любое значение. Значение двоичного числа определяется относительной позицией каждого бита и наличием единичных битов. Ниже показано восьмибитовое число, содержащее все единичные биты:

значения:  128  64  32  16  8  4  2  1
биты:    1   1   1   1  1  1  1  1

Самая правая цифра имеет весовое значение 1, следующая цифра влево - 2, следующая - 4 и т.д. Общая сумма для восьми единичных битов в данном случае составит 255:

(1+2+4+8+16+32+64+128=255)

Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:

512	256	128	64	32	16	8	4	2	1

Начиная с цифры 1 все цифры умножаются на два.

• Первый вариант: Преобразование десятичных чисел в двоичные

Допустим, нам нужно перевести число 17 в двоичное. Согласно таблице степеней оснований (см. выше) 17=16+1. Значит на место значимых цифр 16 и 1 ставим 1 - остальные нули. Получаем 17=10001

512	256	128	64	32	16	8	4	2	1
0       0       0       0       0       1       0       0       0       1

• Второй вариант: Преобразование десятичных чисел в двоичные

Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :

19 /2 = 9  с остатком 1
9  /2 = 4  c остатком 1
4  /2 = 2  с остатком 0
2  /2 = 1  с остатком 0
1  /2 = 0  с остатком 1

Итак, мы делим каждое частное на 2 и записываем остаток в начало двоичной записи. Продолжаем делить на 2 частные от деления до тех пор, пока частное не станет равным 0. В результате получаем число 19 в двоичной записи: 10011.

• Первый вариант: Преобразование двоичных чисел в десятичные

В обратную сторону нужно десятичные сложить, основываясь на таблице степеней основания 2.

Компьютер выполняет арифметические действия только в двоичном формате. Поэтому, необходимо знать правила сложения в двоичной системе исчисления. Напомним их:

0 + 0 = 0
1 + 0 = 1
1 + 1 = 10

Давайте рассмотрим использование этих правил на конкретном примере.

• Пример: сложить числа 65 и 42, представленные в двоичной системе исчисления.

В десятичной системе исчисления все осуществляется достаточно просто: 65+42=107. Для сложения этих чисел в двоичной системе исчисления нужно сначала перевести их в эту систему, например, как показано на рисунке: Таким образом, получаем: 65 в 10-ой системе = 01000001 в 2-ой системе. Обратите внимание на то, что ведущий ноль в двоичном представлении числа добавлен для дополнения двоичного представления до восьми бит. Аналогично: 42 в 10 = 00101010 в 2. Выполним сложение этих чисел:

   01000001
+
   00101010
   --------
   01101011

Можете перепроверить и убедиться, что 01101011 в 2=107 в 10:

0*27+1*26+1*25+0*24+1*23+0*22+1*21+1*20 = 64+32+8+2+1 = 107

• Вычитание

Для выполнения операции вычитания последнее заменяется сложением, а в качестве второго слагаемого берется противоположное число. Например, пусть надо выполнить вычитание: 65 - 42. Заменим его сложением: 65 + (-42).

27 /16 = 1  с остатком 11
11 /16 = 0  c остатком 1

И того получим 1B.

Рассмотрим несколько простых примеров шестнадцатеричной арифметики. Следует помнить, что после шестнадцатеричного числа F следует шестнадцатеричное 10, что равно десятичному числу 16:

6+4=A 
5+8=D
F+1=10 
F+F=1E 
10+10=20 
FF+1=100