Сортировка вставками — простой алгоритм сортировки. Хотя этот алгоритм сортировки уступает в эффективности более сложным (таким как Быстрая сортировка), у него есть ряд преимуществ:

• прост в реализации;
• эффективен на небольших наборах данных, на наборах данных до десятков элементов может оказаться лучшим;
• эффективен на наборах данных, которые уже частично отсортированы;
• это устойчивый алгоритм сортировки (не меняет порядок элементов, которые уже отсортированы);
• может сортировать список по мере его получения;
• не требует временной памяти, даже под стек.

Популярные алгоритмы сортировки. Что такое алгоритм?

Для реализации алгоритма "Сортировка вставками" будем использовать язык CPP.

#include <iostream>
#include <stdlib.h>
#include <time.h>
 
using namespace std;
 
template <class T>
void insertSort(T a[], long size) {
	T x;
	long i, j;
 
	for(i=0;i<size;i++){  // цикл проходов, i - номер прохода
		x=a[i];
 
		// поиск места элемента в готовой последовательности 
		for (j=i-1;j>=0&&a[j]>x;j--)
				a[j+1]=a[j];  	// сдвигаем элемент направо, пока не дошли
 
		// место найдено, вставить элемент
		a[j+1] = x;
	}
}
 
void main(){
	srand(time(NULL));
	const long SIZE=10;
	int ar[SIZE];
 
	// до сортировки
	for(int i=0;i<SIZE;i++){
		ar[i]=rand()%100;
		cout<<ar[i]<<"\t";
	}
	cout<<"\n\n";
	shakerSort(ar,SIZE);
 
	// после сортировки
	for(int i=0;i<SIZE;i++){
		cout<<ar[i]<<"\t";
	}
	cout<<"\n\n";
}

Хорошим показателем сортировки является весьма естественное поведение: почти отсортированный массив будет досортирован очень быстро. Это, вкупе с устойчивостью алгоритма, делает метод хорошим выбором в соответствующих ситуациях. Однако, алгоритм можно слегка улучшить. Заметим, что на каждом шаге внутреннего цикла проверяются 2 условия. Можно объединить из в одно, поставив в начало массива специальный "сторожевой элемент". Он должен быть заведомо меньше всех остальных элементов массива.

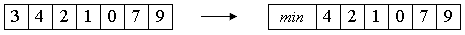
Тогда при j=0 будет заведомо верно a[0] ⇐x. Цикл остановится на нулевом элементе, что и было целью условия j>=0. Таким образом, сортировка будет происходить правильным образом, а во внутреннем цикле станет на одно сравнение меньше. Однако, отсортированный массив будет не полон, так как из него исчезло первое число. Для окончания сортировки это число следует вернуть назад, а затем вставить в отсортированную последовательность a[1]…a[n].